Herleitung verschiedener Geometrien mit Hilfe der Differentialgeometrie von geometrischen Flächen und Körpern mit der Integralberechnung

Herzlich willkommen auf dieser Homepage die zum Erlernen der Integralberechnung dienen soll. Bei den Berechnungen der Geometrien wird jedes Mal gleich Vorgegangen. Erst werden die Variablen die der Berechnung des Flächendifferentials dA oder des Volumendifferentials dV dienen berechnet und anschließend für die Flächen- oder Volumenberechnung mit Hilfe der Integralberechnung berechnet. Die Flächen- und Volumendifferentiale sowie alle anderen Variablen sind aus den Zeichnungen ersichtlich. Der Vorgang ist jedes Mal der gleiche.

Man muss nur wissen, dass sich hinter dem Integralzeichen auch ein Summenzeichen verbirgt was dem Anwender sagt das die Flächen- und Volumenelemente dA oder dV über die Gesamtfläche A oder dem Gesamtvolumen V aufsummiert werden müssen.

Die Variablen z.B. a(x) oder r(x) die zur Berechnung des Flächendifferentials oder des Volumendifferentials benötigt werden, müssen häufig mit dem 2. Strahlensatz berechnet werden.

Bei diesem Berechnungsverfahren wurde zur Flächen- und Volumenberechnung immer nur eine Variable x verwendet um das Berechnungsverfahren so einfach wie nur möglich zu erlernen.

Viel Spaß beim Lernen!

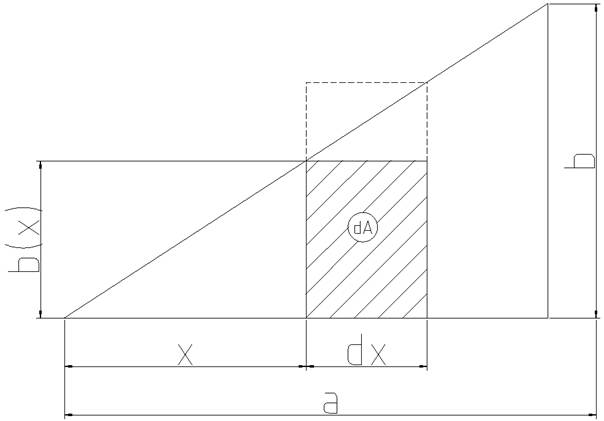
Beim Integrieren bzw. beim Aufsummieren der Flächenelemente dA füllt das Integral die leere Fläche über dem Streifen dA aus und schneidet die überstehende Fläche des Streifens ab.

Ein Bild, das Diagramm, Reihe, parallel, technische Zeichnung enthält.

Automatisch generierte Beschreibung

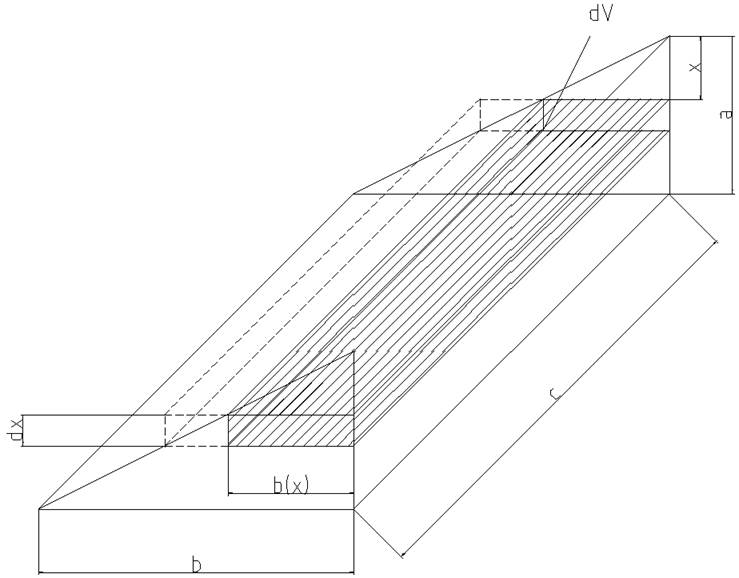
Beim Integrieren bzw. beim Aufsummieren der Volumenelemente dV füllt das Integral das Volumen über der Scheibe dV aus und und schneidet das überstehende Volumen der Scheibe ab.

Ein Bild, das Entwurf, Zeichnung, Diagramm, Reihe enthält.

Automatisch generierte Beschreibung

Betrachtet man ein Volumenelement dV eines Körpers so ergibt sich daraus der mathematische Zusammenhang:

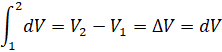
dV wäre dann das zu integrierende Volumenelement!